“Enrichment beyond the classroom”
GREECE and ITALY
join a Mediterranean math-collaboration!
etwinning project 2015-2016

Sun activities
Katerina Atmatzidou, math teacher Lykeio Schimatariou
Matilde Aimetta, Math teacher Vallauri Fossano
and the super mixed greek-italian team!

Sun activities
"You ask me to describe the Sun activity?
Here are the words to describe it: Maths, Theory of similar triangles, collaboration, out of the class,awsome, fun, understand , learn, real life,action, please do it again!"
team Bonds
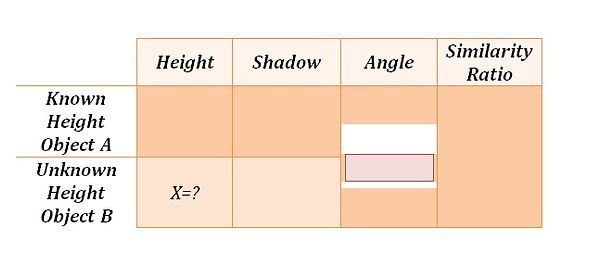
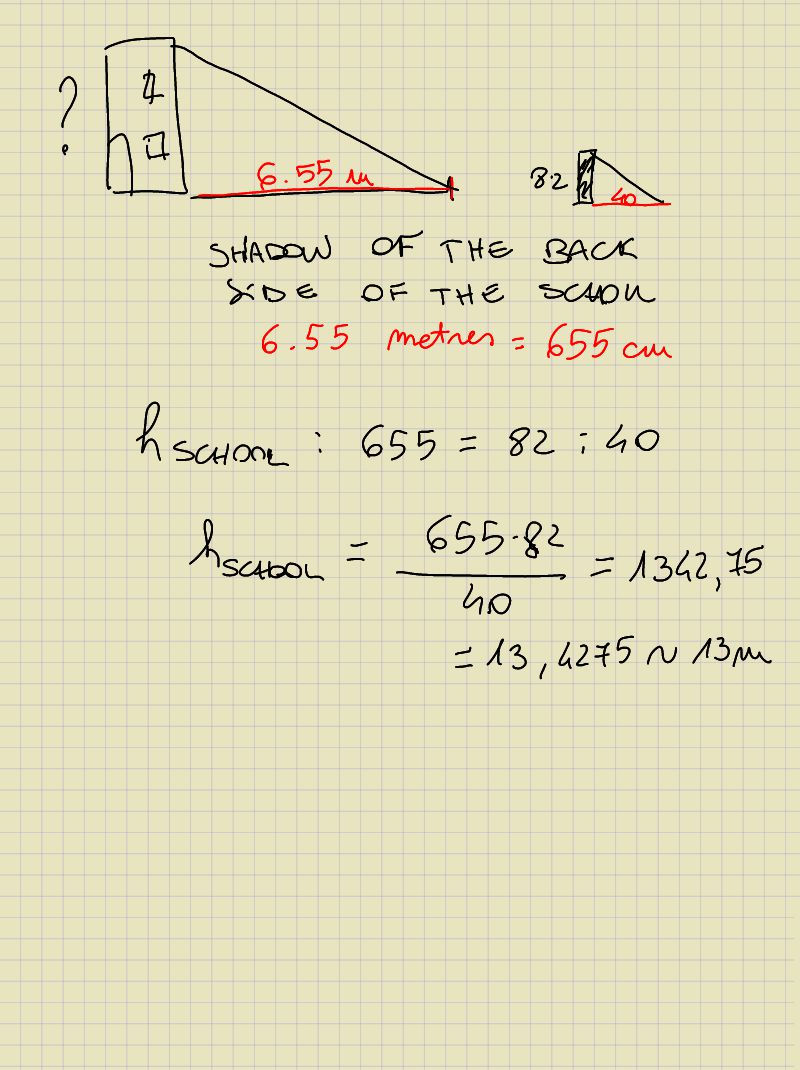
Indirectly calculate the height of an object out in the sun, using similar triangles principles.
STEP1 :
Collect Data out in the sun
Find out the Height of an object A which is easy to be measured and the length of its shadow. Measure the length of the shadow of object B . Calculate the Angle of the sun using trigonometry, until the figure will follow according to the data you have collected.
STEP2:
THE ACTIVITY USING THE GEOGEBRA APP
You may adjust the Height of the objects and the Angle of the sun, until the figure will follow according to the data you have collected:
1. Adjust the height of the object you know it's height (the red line).
2. Adjust the angle of the sun, so that the shadow of that object will be the same as you've collected.
3. Adjust the height of the object you don't know it's height (the Green line), so that it's shadow will reach that you've measured.
https://www.geogebra.org/m/q8NbdyKe?doneurl=%2Fmaterials
STEP3:
THE Sun ACTIVITY
using
Theory of similar triangles
Theory of similar triangles principles
You can study the topic from the link below and then answer the following questions.
http://www.mathopenref.com/similartriangles.html
Now is your turn!
1.Can you prove the 2 triangles in the figure are similar? (Remember that all sun rays are parallel to each other and the ground could be considered as one line)
2. Can you find the similarity ratio between the 2 triangles?
3. Can you find The Height of the Green Line (X) ?
4. What will change if you change the sun ray's angle? what will stay the same?
5. Can you find practical limitations as to when this sort of measurement will actually work? (For example - It will work only at daytime)



We created an activity flipping book for the first steps of our study.Feel free to download and print.






New skills to use for hidden maths in school activities.


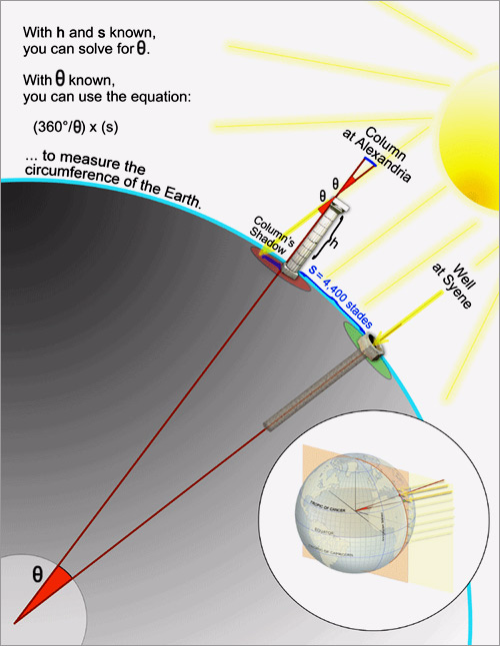
Eratosthenes measured the circumference of Earth around 240 BC, based on the fact that the Sun appears in the zenith at noon on the summer solstice, in Syene (modern Aswan). At the same time, in Alexandria, the angle of the shadow of a post was slightly more than 7° (you can vary this parameter in this Demonstration), which is roughly 1/50 of the circumference (7/360 ≈ 0.0194444); the distance between the cities is 5000 stadia (an ancient Greek unit, about 185 meters) or about 925 km. The calculation gives 925/.02 ≈ 46250 km, a value very near today's value of 40000 km, with an error of 16%; an amazing feat for the epoch in which he lived.






Analemma


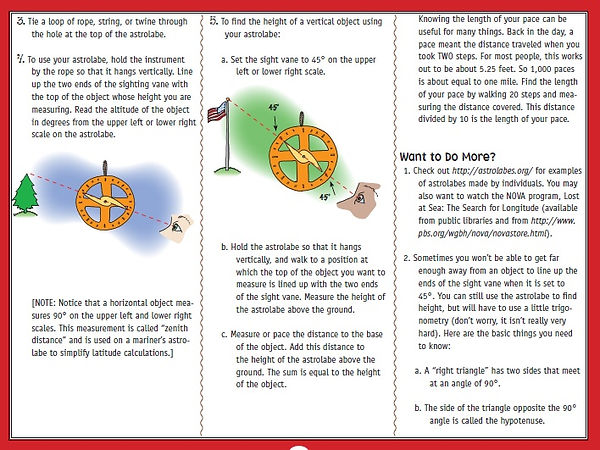
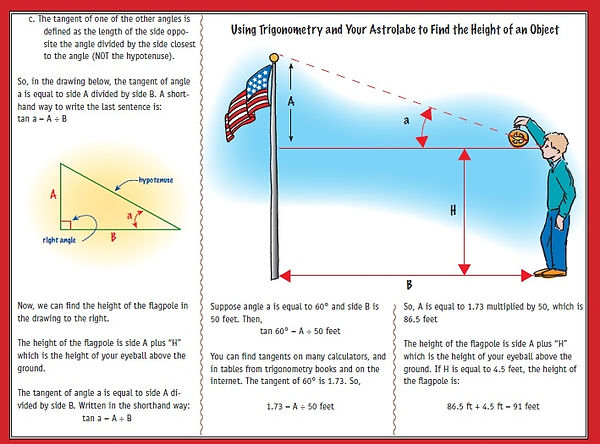
Astrolabe


GEOGEBRA app
Math Investigation Sun Activity: Similar triangles
GEOGEBRA app
Math Investigation Sun Activity: ERATOSUENIS
Outdoor Math!
Math Investigation Sun Activity: Similar triagles, measurments and calculations


Describe your image.

Describe your image.
Describe your image.

Describe your image.

Describe your image.

Describe your image.


Describe your image.

Describe your image.

Describe your image.

Describe your image.

Describe your image.

Describe your image.
Click on the picture to watch a funny story through a sun activity!