


“Enrichment beyond the classroom”
GREECE and ITALY
join a Mediterranean math-collaboration!
etwinning project 2015-2016

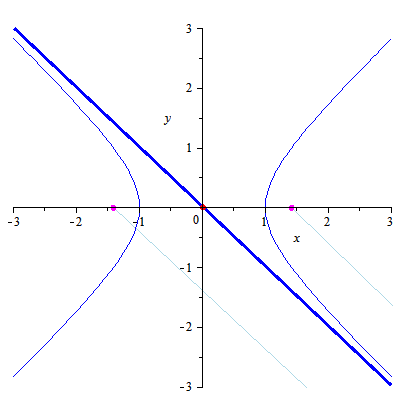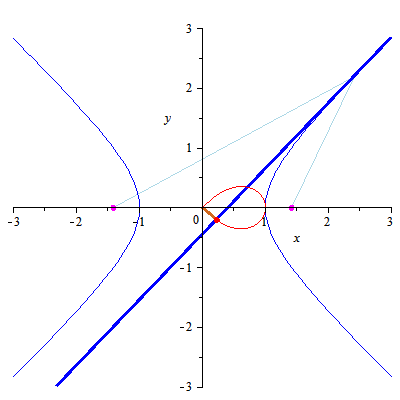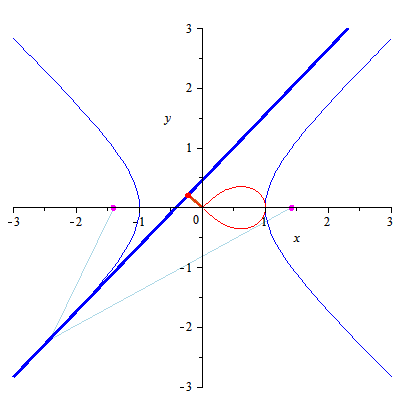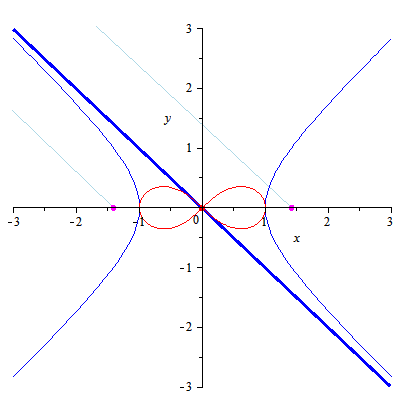
The lemniscate, also called the lemniscate of Bernoulli, is a polar curve
whose most common form is the locus of points the product of whose
distances from two fixed points (called the foci) a distance 2a away is
the constant a2. This gives the Cartesian equation
(1)
where both sides of the equation have been squared. Expanding and simplifying then gives
(2)
Jakob Bernoulli published an article in Acta Eruditorum in 1694 in which he called this curve the lemniscus (Latin for "a pendant ribbon"). Bernoulli was not aware that the curve he was describing was a special case of Cassini ovals which had been described by Cassini in 1680. The general properties of the lemniscate were discovered by G. Fagnano in 1750 (MacTutor Archive). Gauss's and Euler's investigations of the arc length of the curve led to later work on elliptic functions.
The most general form of the lemniscate is a toric section of a torus
cut by a plane . Plugging in and rearranging gives the equation
In the special case (and rewriting as ), this becomes
which is the same form obtained in equation (1).
The two-center bipolar coordinates equation with origin at a focus is
Switching to polar coordinates gives the equation
usually simply written
where is a constant (differing from the torus radius by a factor of ). Note that this equation is only defined for angles and . The parametric equations for the lemniscate with width are
The bipolar equation of the lemniscate is
and in pedal coordinates with the pedal point at the center, the equation is
The lemniscate can also be generated as the envelope of circles centered on a rectangular hyperbola and passing through the center of the hyperbola (Wells 1991).
The lemniscate is the inverse curve of the hyperbola with respect to its center.
The area of the lemniscate is

Read the magazine below and then test your knowledge by the math online crossword that we designed.
Because... learning can be fun!
Every time you restart the crossword game, a new crossword is on your screen. Go for it, have fun, we collaborate and study using an online game!
by t.c
The cover of the magazine: Math Investigation Volume: Infinity
Click on the left button to read the flipping e-magazine
We found this Ted Ed video about infinity been uploaded in youtube as we were searching in internet...
What is common between the Infinity and a ship?
Easy answer...
Let change hotel to ... ship!
Only finitely many rooms in an infinite ship!
It is the same thought....
Let your imagination limit to infinity!
Watch the scene of an old film "Murder Ahoy", based on miss Marple Stories from Agatha Christie, 1964
Different abilities... Different engagement...
Different kind of involvement....
Trying to find out new strategies on how to involve students of every level of ability and keep them engaged in Math lessons through the use of collaborative activities.
Actually "Math Investigation" project uses all students' abilities. Some of them were the artists of the team.
There is ...room for all dreams!
You can see the art creations in these posters for infinity mission!



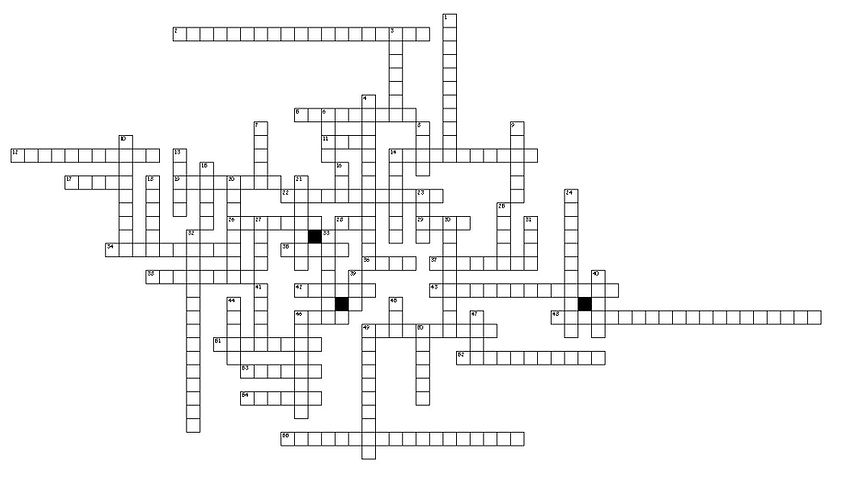
Across
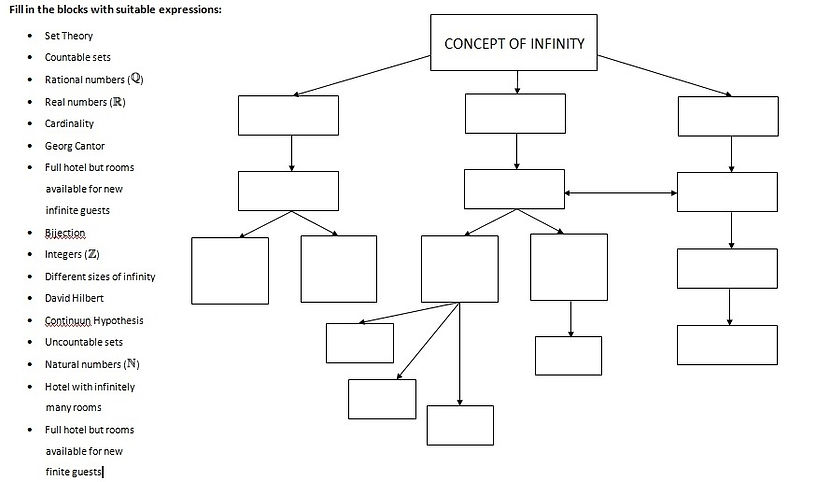
2. The cardinality of the real numbers is the next bigger cardinality after the cardinality of the natural numbers.
5. The mathematician who discovered the existence of unprovable statements like the continuum hypothesis
11. Coming after all others in time or order; final.
12. The number of elements in a set, whether the set is finite or infinite. Note: Not all infinite sets have the same cardinality.
14. A positive integer which has only 1 and the number itself as factors. For example, 2, 3, 5, 7, 11, 13, etc.
17. Two times; on two occasions.
19. An attribute, quality, or characteristic of something.
22. The German mathematician who tried to explain some of the properties of infinity using a hotel with infinitely many rooms.
26. Extend over so as to cover partly. You can say, for example: ‘the curtains overlap at the centre when closed’.
28. A group of numbers, variables, geometric figures, or just about anything.
29. On one occasion or for one time only.
34. A statement that cannot be proved.
35. The result of raising a base to an exponent.
36. Coming immediately after the previous one.
37. All positive and negative whole numbers (including zero). That is, the set {... , –3, –2, –1, 0, 1, 2, 3, ...}.
38. A "number" which indicates a quantity, size, or magnitude that is larger than any real number.
42. An arithmetical value, expressed by a word, symbol, or figure, representing a particular quantity and used in counting and making calculations.
43. The numbers used for counting. That is, the numbers 1, 2, 3, 4, etc.
46. Containing or holding as much or as many as possible; having no empty space.
48. Proving a conjecture by assuming that the conjecture is false. If this assumption leads to a contradiction, the original conjecture must have been true.
49. The part of a conditional after If and before then.
51. Straight up and down. As an example, we can consider a wall.
52. The first mathematician to realize that there are different kinds, different sizes of infinity.
53. Describes a set which does not have an infinite number of elements. That is, a set which can have its elements counted using natural numbers. Formally, a set is finite if its cardinality is a natural number.
54. A mark or character used as a conventional representation of an object, function, or process, e.g. the letter or letters standing for a chemical element or a character in musical notation.
55. Writing an integer as a product of powers of prime numbers.
Down
1. Describes a set which contains more elements than the set of integers. Formally, an uncountably infinite set is an infinite set that cannot have its elements put into one-to-one correspondence with the set of integers. For example, the set of real numbers is uncountably infinite.
3. Think or assume that something is true or probable.
4. A logical incompatibility between two or more propositions.
6. One of a set of explicit or understood regulations or principles governing a particular area of activity.
7. A person staying at a hotel.
8. A network of lines that cross each other to form a series of squares or rectangles.
9. Quick to understand, learn, and apply ideas; intelligent.
10. A function between the elements of two sets, where every element of one set is paired with exactly one element of the other set, and every element of the other set is paired with exactly one element of the first set. There are no unpaired elements.
13. Containing nothing; not filled or occupied.
14. An inquiry starting from given conditions to investigate or demonstrate a fact, result, or law.
15. Find all solutions to an equation, inequality, or a system of equations and/or inequalities.
16. An integer that is not a multiple of 2.
18. Any integer which divides evenly into a given integer.
20. x in the expression ax.
21. A seemingly absurd or contradictory statement or proposition which when investigated may prove to be well founded or true.
23. A part or division of a building enclosed by walls, floor, and ceiling.
24. All numbers on the number line. This includes (but is not limited to) positives and negatives, integers and rational numbers, square roots, cube roots , π (pi), etc.
25. A continuous area which is free, available, or unoccupied.
27. An integer that is a multiple of 2.
30. Describes the cardinality of a countably infinite set. For example, the set of natural numbers is countably infinite. Aleph null (א0) is the symbol for this.
31. A mathematical operation of addition.
32. All positive and negative fractions, including integers and so-called improper fractions. Formally, rational numbers are the set of all real numbers that can be written as a ratio of integers with nonzero denominator.
33. Relating to or denoting a system of numbers and arithmetic based on the number ten, tenth parts, and powers of ten.
39. Produced, introduced, or discovered recently or now for the first time; not existing before.
40. A convincing demonstration that some mathematical statement is necessarily true.
41. Any of the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 used to write numbers.
44. An establishment providing accommodation, meals, and other services for travelers and tourists, by the night.
45. A break or hole in an object or between two objects.
46. A numerical quantity that is not a whole number.
47. A thing’s dimensions or magnitude; how big something is.
49. Perfectly flat and level. For example, we can think to the horizon. So is the floor.
50. A contemplative and rational type of abstract or generalizing thinking, or the results of such thinking.
Thoughts......

"Math is a subject that most of the students find it very difficult to study and understand. Most of the members of both teams, from Italy and Greece, attempt to aproache some of the ...infinity affairs by an a new way. Games always is our favorite part. So we designed some games to make studing infinity more fun! They call it... Gamification!!!
It was an excellent idea, as eTwinning let us express our creativity through games! And guess! We explore new etools and find out that our imagination has no limits! Thanks eTwinning for inspiration!
For eTwinning project: Math investigation. Mission: Infinity"
M.K, Greece

GAME DESIGNED BY our team.
Light the ..picture!
Movie... surprise!
When we desided to involve with the infinity affairs in this math investigation mision, we had no idea about the new film
" The Man Who Knew Infinity "
What a coincident! So we had to emmbeed the trailer of the Movie in youtube. Read a brief notice about the film and then watch it. Why?
Because "Math Investigation":Mission Infinity" can be fun too!!!
The Man Who Knew Infinity Official Trailer #1 (2016) - Dev Patel, Jeremy Irons Movie HD
Growing up poor in Madras, India, Srinivasa Ramanujan Iyengar earns admittance to Cambridge University during WWI, where he becomes a pioneer in mathematical theories with the guidance of his professor, G.H. Hardy.

